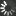Inhibitory
$a_{ii}$
$a_{ie}$
$\tau_i$
$\theta_i$
$g_i$
$\sigma_{i}$
$N_i$
$\alpha_i$
$\beta_i$
Excitatory
$a_{ee}$
$a_{ei}$
$\tau_e$
$\theta_e$
$g_e$
$\sigma_{e}$
$N_e$
$\alpha_e$
$\beta_e$
Time stepping
$\Delta t$
Skip
Stimulus
$A$
Presets
E-cell firing rate ∈[0,1]
I-cell firing rate ∈[0,1]
E/I trajectories in phase spacePeripheral region
E-cell firing rate
I-cell firing rate
E/I trajectories in phase spaceStimulated region
Click to start
Wave State Demonstration
This demonstration is designed to illustrate a hypotehtical wave mode seen during optogentic stimulation in motor cortex. In this mode, the stimulated region forces damped traveling waves in the periphery at a ratio of 2:1. Additionally, there is instability inside the stimulated region, leading to traveling waves across the stimulation area that originate at the boundary. The Stimulated region has a radius of 30 pixels, the stimulus mask has been smoothed with a Gaussian kernel with a standard deviation of 4 piexls, given the stimulated region a soft boundary. Heterogeneity is added to the time constants (in a somewhat hacked way that I can explain or try to clean up), and is also smoothed with a Gaussian kernel of 4 pixels. These new additions are not reflected in the equations.
Simulation
\[\textrm{E-cells: } \tau_e \dot{U_e} = -U_e + f( a_{ee} \cdot K_e \star U_e - a_{ie} \cdot K_i \star U_i - \theta_e + g_e S(t) - \beta_e V_e)\]
\[\textrm{I-cells: } \tau_i \dot{U_i} = -U_i + f( a_{ei} \cdot K_e \star U_e - a_{ii} \cdot K_i \star U_i - \theta_i + g_i S(t) - \beta_i V_i )\]
\[\textrm{E-cell adaptation: } \alpha_e \dot{V_e} = U_e - V_e \]
\[\textrm{I-cell adaptation: } \alpha_i \dot{V_i} = U_i - V_i \]
\[\textrm{Interaction kernel (normalized to 1): } K_{e,i}(x,y) \propto \exp(\frac{1}{2} \frac{x^2}{\sigma_{x\,e,i}^2}+\frac{1}{2} \frac{y^2}{\sigma_{y\,e,i}^2})\]