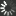Flicker

Inhibitory

$\tau_i$

$a_{ie}$

$\theta_i$

Excitatory

$\tau_e$

$a_{ee}$

$a_{ei}$

$\sigma_e$

$\theta_e$

Refractory

$\tau_a$

$\gamma_a$

$\beta_e$

Time stepping

$\Delta t$

Driving

$N_e$

Presets

E-cell firing rate ∈[0,1]

I-cell firing rate ∈[0,1]

E/I trajectories in phase space
Steady-state adaptation

Firing Rate Red = E, Green = Ie

Adaptation Red = E, Green = I

E/I trajectories in phase space
Without adaptation

Click to start

Wilson-Cowan with diffusive coupling

Info details here. TODO.

Simulation

\[\tau_e \dot U_e = - U_e + f\left[ a_{ee} \left(\sigma_e \nabla^2 U_e + U_e \right) - a_{ei} U_i - \beta V_e - \theta_e \right]\] \[\tau_i \dot U_i = - U_i + f \left[ a_{ei} U_e - \theta_i \right]\] \[\tau_a \dot V_e = (U_e - V_e) \cdot (\gamma H(U_a - U_e) + 1)\]